Concept of diffusion: Laws of diffusion, Steady state diffusion, Measurement of diffusion and MCQs for GPAT, NIPER, Pharmacist and Drug Inspector exam
Diffusion is defined as the mass transfer of individual molecules of a substance (diffusant), brought about by random molecular motion along a concentration gradient. Diffusion is caused by the Brownian motion of atoms or molecules and results in the decrease in the free energy of the system. In solids, diffusion progresses at a rate of micrometer per second; in liquids, its rate is typically fractions of millimeter per second; in gases, diffusion is a fairly fast process with a typical rate of centimeter per second. Free diffusion of the substance through liquids, solids and the membranes are processes of considerable interest in the pharmaceutical sciences. The diffusion phenomenon applying in the pharmaceutical sciences includes:
- Absorption and elimination of drug molecules in living systems.
- Permeation of drug molecules through the skin, cornea or buccal mucosa.
- Release of the drug from the dosage form.
- Evaluation of antimicrobial activity.
- As a mechanism of mixing.
- Filtration and integrity testing of filters.
LAWS OF DIFFUSION:
Diffusion can be studied by observing the flow of molecules through a barrier or membrane, which occurs either by simple molecular permeation or by movement via pores or channels.

Fig 1 – Schematic representation of the diffusion process. (taken from researchgate.net)
Fick’s First Law – Fick’s first law states that flux is proportional to the concentration gradient across the barrier, i.e.
J = -DdC/dx (1)
where D is the diffusion coefficient of a penetrant (or diffusant) (m2 s–1 or cm2 s–1), C the concentration (kg m–3 or g cm–3), x the distance if the movement is perpendicular to the surface of the barrier (m or cm) and J the flux (kg m–2 s–1 or g cm–2 s–1).
The flux is the quantity of a material flowing through a unit cross-section of a barrier in unit time and is denoted as
J = dM/Sdt (2)
where M is the amount of material flowing (kg or g or mole), S the cross-sectional area (m2 or cm2) and t the time (s).
Eq. (1) represents Fick’s first law. The negative sign in Eq. (1) denotes that diffusion occurs in a direction opposite to that of increasing concentration, i.e. diffusion occurs in the direction of decreasing concentration of the diffusant, and thus flux is always a positive quantity.
According to Fick’s first law, movement of mass will cease when no concentration gradient remains between two positions or when dC/dx approaches zero.
Fick’s Second Law – Fick’s second law gives the equation for mass transport that highlights the change in diffusant concentration at a particular region in a system rather than mass diffusing across a unit area of a barrier in unit time. The concentration of the diffusant in a particular volume element changes only due to the net flow of diffusing molecules into or out of the region. The concentration of a diffusant in the volume component changes with time (‘C/‘t) as the flux or amount diffusing changes with distance (‘J/‘x) in the x direction, i.e.
dC/dt = -dJ/dx (3)
Differentiating Fick’s first law of Eq. (1), with respect to x, we get
-dJ/dx = -Dd2C/dx2 (4)
Substituting Eq. (4) into Eq. (3), we obtain a relation for Fick’s second law as follows:
dC/dt = -Dd2C/dx2 (5)
Fick’s second law states that the change in concentration with time in a particular region is proportional to the change in concentration gradient at that point in the system. It relates the temporal and spatial distributions of concentration of the system.
Steady-State Diffusion:
At steady-state, there is no change of concentration with time. Steady-state condition is characterized by the condition
dC/dt = 0 (6)
Measurement of Diffusion:
Diffusion cells are used to carry out the measurements of diffusion. A diffusion cell consists of a donor chamber and a receptor chamber with a membrane fixed in between. The diffusion cell, also known as Franz diffusion cells, has either vertical or horizontal configurations.
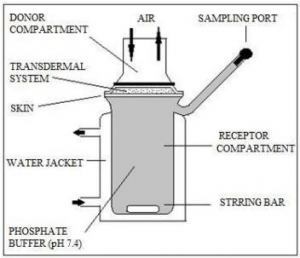
Fig 2 – Schematic representation of a vertical Franz diffusion cell. (taken from Franz diffusion cell.method. The glass diffusion cell/download scientific diagram)
The donor chamber of a diffusion cell contains a known concentration of a solute and this solution is referred to as the donor solution. The receptor chamber contains the receptor solution on the other side of the membrane. The receptor chamber usually contains the solvent of the donor solution but is completely devoid of the solute. It is maintained at a temperature of 37 ± 0.5°C using a water jacket. The receptor solution is continuously stirred by means of a stirring bar. When the diffusion experiment starts, the solute from the donor solution diffuses through the membrane into the receptor solution. The receptor solution is periodically removed for analysis from a sampling port located in the receptor chamber to estimate the concentration of the diffusant migrated from the donor solution into the receptor solution. The receptor solution is replaced with a new receptor solution after every sampling to keep the volume of receptor solution constant during the experiment. The results of the analysis are used to calculate the diffusion coefficient and the flux.
Multiple choice questions:
1.Diffusion is defined as the mass transfer of individual molecules of a substance (diffusant), brought about by random molecular motion along a concentration gradient.
a)true
b)false
2.Diffusion is caused by the _____ of atoms or molecules
a)dissolution
b)brownian motion
c)solubility
d)turbidity
3.In solids, diffusion progresses at a rate of
a)micrometre per second
b)millimetre per second
c)centimetre per second
d)all of these
4.In liquids, rate of diffusion is typically fractions of
a)micrometre per second
b)millimetre per second
c)centimetre per second
d)all of these
5.In gases, diffusion is a fairly fast process with a typical rate of
a)micrometre per second
b)millimetre per second
c)centimetre per second
d)all of these
6.The diffusion phenomenon applying in the pharmaceutical sciences includes:
a)Absorption and elimination of drug molecules in living systems
b)Permeation of drug molecules through the skin, cornea or buccal mucosa
c)Release of the drug from the dosage form
d)all of these
7.Diffusion can be studied by observing the flow of molecules through a barrier or membrane, which occurs by
a)simple molecular permeation
b)movement via pores or channels
c)both of these
d)only a
8.Fick’s first law states that flux is proportional to the concentration gradient across the barrier
a)true
b)false
9.Which of the following equation represents Fick’s first law?
a)J = -DdC/dx
b)J = dM/Sdt
c)dC/dt = -Dd2C/dx2
d)dC/dt = 0
10.The flux is the quantity of a material flowing through a unit cross-section of a barrier in unit time and is denoted as
a)J = -DdC/dx
b)J = dM/Sdt
c)dC/dt = -Dd2C/dx2
d)dC/dt = 0
11.What does negative sign in Fick’s first law of diffusion eqaution denotes?
a)diffusion occurs in a direction opposite to that of increasing concentration
b)diffusion occurs in the direction of decreasing concentration of the diffusant
c)only b
d)both of these
12.Flux is always a _____ quantity.
a)positive
b)negative
c)neutral
d)may be positive as well as negative
13.A relation for Fick’s second law is as follows
a)J = -DdC/dx
b)J = dM/Sdt
c)dC/dt = -Dd2C/dx2
d)dC/dt = 0
14.Steady-state condition is characterized by the condition
a)J = -DdC/dx
b)J = dM/Sdt
c)dC/dt = -Dd2C/dx2
d)dC/dt = 0
15.Which of the following is used for measurement of diffusion?
a)viscometer
b)basket type apparatus
c)flow through cell
d)franz diffusion cell
Solutions:
- a)true
- b)brownian motion
- a)micrometre per second
- b)millimetre per second
- c)centimetre per second
- d)all of these
- c)both of these
- a)true
- a)J = -DdC/dx
- b)J = dM/Sdt
- d)both of these
- a)positive
- c)dC/dt = -Dd2C/dx2
- d)dC/dt = 0
- d)franz diffusion cell
References:
- Gaurav K. Jain Theory and Practice of Physical Pharmacy, 1st edition 2012 Elsevier, page no. 266-271.
- Martins Physical Pharmacy, 6th edition 2011, page no. 415-422.
List of Successful GPATINDIAN CANDIDATES
Participate in Online FREE GPAT TEST: CLICK HERE
Participate in Online FREE Pharmacist TEST: CLICK HERE
Participate in Online FREE Drug Inspector TEST: CLICK HERE